利用灵敏性分析确定模型参数的敏感性
灵敏性分析能够量化各因素对模型输出的影响程度。当模型存在多个待定参数时,可以将这些参数作为分析对象,通过灵敏性分析识别出对模型结果影响较大的关键参数。对这些高敏感参数进行针对性识别,能有效提升模型的精度和可靠性,尤其适用于参数众多的复杂模型。
主要的灵敏性分析方法
局部灵敏性分析(Local Sensitivity Analysis)
局部灵敏性分析关注输入参数在某一特定点附近的微小变化对模型输出的影响,通常通过计算偏导数或在参数值附近做小幅度扰动来实现。例如,单变量变化法(One-At-a-Time, OAT)、微分法(计算偏导数)。这类方法计算简单,适合快速了解模型对单个参数的局部响应特性。
$$ S_i^{\text{OAT}} \approx \frac{y(x_1, …, x_i+\Delta x_i, …, x_n) - y(x_1, …, x_i, …, x_n)}{\Delta x_i} $$
- 优点:计算量小,易于实现。
- 缺点:只反映参数在特定点的局部影响,无法揭示参数在全范围内的变化效应,且忽略参数间的相互作用。
- 适用于模型简单、参数变化范围有限的情况,快速了解模型对单个参数的局部响应特性。
全局灵敏性分析(Global Sensitivity Analysis)
全局灵敏性分析考察输入参数在其整个取值范围内变化对模型输出的影响,能够捕捉参数间的非线性关系和相互作用,提供更全面的敏感性评估。
Morris 方法
Morris 方法通过在参数空间内进行一系列有设计的“基本步长”扰动,计算每个参数的平均效应和标准差,从而区分参数的总体影响与非线性或交互作用。
- 优点:计算量与参数数量呈线性关系,计算效率较高,适合高维参数空间,能够快速筛选出重要参数。
- 缺点:结果主要用于定性排序,通常不适用于精确定量分析。
具体步骤如下:
首先,计算基本效应(elementary effect):
$$ EE_i = \frac{y(x_1, …, x_i + \Delta, …, x_k) - y(x_1, …, x_i, …, x_k)}{\Delta} $$
其中,$\Delta$ 是参数的扰动步长,$i=1,2,\ldots,k$ 表示第 $i$ 个参数。对于每个参数 $i$,在 $R$ 条不同采样路径上计算多个基本效应 $EE_i^{(r)}$,$r=1,2,\ldots,R$。
接着,计算均值,衡量参数的平均效应:
$$ \mu_i = \frac{1}{R} \sum_{r=1}^R EE_i^{(r)} $$
由于非单调函数中基本效应可能正负抵消,通常采用绝对值的均值:
$$ \mu_i^* = \frac{1}{R} \sum_{r=1}^R |EE_i^{(r)}| $$
同时计算标准差,反映参数效应的非线性和交互作用:
$$ \sigma_i = \sqrt{\frac{1}{R-1} \sum_{r=1}^R \left(EE_i^{(r)} - \mu_i\right)^2} $$
其中,$\mu_i^*$ 越大表示参数 $x_i$ 对模型输出影响越显著,$\sigma_i$ 越大则表明该参数的效应存在较强的非线性或与其他参数的交互作用。
具体方法和实现细节可参考该文档,需注意:
- 对模型输入和输出进行无量纲标准化,以保证灵敏性结果的可比性;
- Morris 方法依赖特殊的采样设计,常见的有轨迹设计(Trajectory Design)和径向单因素扰动设计(Radial OAT Design);
- 可通过在 $\sigma_i$ - $\mu_i^*$ 平面绘制散点图,直观区分重要参数与非重要参数。
Sobol 方法
Sobol 方法基于方差分解原理,将模型输出的总方差分解为各输入参数及其交互作用对方差的贡献份额,从而定量评估每个参数的主效应和总效应灵敏度指数。
- 优点:理论基础严谨,能够全面捕捉参数的线性、非线性以及多参数间的交互效应,提供精确的定量灵敏度指标。
- 缺点:计算量较大,通常需要大量的模型运行和采样,计算成本较高。
模型输出的总方差为:
$$ V = \mathrm{Var}[Y(\mathbf{X})] $$
其中,$\mathbf{X} = (X_1, X_2, …, X_k)$ 是输入参数向量,$Y$ 是模型输出。
主效应灵敏度指数(First-order Sobol index)定义为:
$$ S_i = \frac{V_i}{V} = \frac{\mathrm{Var}{X_i} \left( \mathbb{E}{\mathbf{X}_{\sim i}}[Y | X_i] \right)}{V} $$
其中,$V_i$ 是参数 $X_i$ 单独对输出方差的贡献,$\mathbf{X}_{\sim i}$ 表示除 $X_i$ 外的所有参数。
总效应灵敏度指数(Total Sobol index)定义为:
$$ S_{T_i} = 1 - \frac{V_{\sim i}}{V} = \frac{\mathbb{E}{\mathbf{X}{\sim i}} \left( \mathrm{Var}{X_i}[Y | \mathbf{X}{\sim i}] \right)}{V} $$
其中,$V_{\sim i}$ 是除参数 $X_i$ 外所有参数的方差贡献,$S_{T_i}$ 衡量参数 $X_i$ 及其与其他参数所有交互作用对输出的总贡献。
Sobol 指数的计算通常基于蒙特卡洛采样,通过设计合理的样本矩阵估计上述方差分量。
FAST 方法(Fourier Amplitude Sensitivity Test)
FAST 方法利用傅里叶变换的思想,将多维参数空间映射到一维频率空间,通过分析模型输出的频谱成分来计算参数的灵敏度,从而提高灵敏度计算的效率。
- 优点:计算效率较高,适合中等维度参数空间,能够较快地估计参数的灵敏度指数。
- 缺点:对高度非线性和高阶参数交互的捕捉能力有限,灵敏度结果可能不够精确。
- 适合输入输出关系较为平滑或近似线性的模型。
将每个输入参数 $X_i$ 以不同的频率 $w_i$ 作为正弦函数的参数,构造参数空间的单一变量函数:
$$ X_i = G_i(\omega s) = \frac{1}{2} + \frac{1}{\pi} \arcsin(\sin(\omega_i s)) $$
其中,$s$ 是一维的频率参数,$\omega_i$ 是为参数 $X_i$ 选定的频率。
模型输出 $Y$ 随着 $s$ 变化,形成一维函数:
$$ Y(s) = f(X_1(s), X_2(s), …, X_k(s)) $$
通过对 $Y(s)$ 进行傅里叶变换,计算不同频率成分的幅值,参数 $X_i$ 的灵敏度指数 $S_i$ 由对应频率成分的方差贡献计算得出:
$$ S_i = \frac{\sum_{m=1}^\infty \left( A_{im}^2 + B_{im}^2 \right)}{\mathrm{Var}[Y]} $$
其中,$A_{im}$ 和 $B_{im}$ 是傅里叶级数中对应频率 $m \omega_i$ 的余弦和正弦系数。
案例:用 Sobol 法分析锂电池 SPMe 的几何参数敏感性
已有一些项目和讨论提及了 PyBaMM 中的参数敏感性分析,例如 Mrzhang-hub/pybamm-param-sensitivities 和 Questions on checking sensitivities 。但是,这些工作主要集中在电化学和材料参数的敏感性分析;而很少涉及几何参数(如电极厚度、隔膜厚度、颗粒半径等)的敏感性分析。这主要是因为几何参数的敏感性分析涉及网格划分和求解器的变化。本案例使用 Sobol 方法,分析锂离子电池单粒子模型(SPMe)中几何参数的敏感性;主要工具为 pybamm(电池建模与仿真)和 salib(敏感性分析);项目仓库为 Mingzefei/battery_model_sensitivity_analysis。
核心库
- PyBaMM (Python Battery Mathematical Modelling):一个开源 Python 电池建模包,支持 DFN、SPM、SPMe 等多种模型。PyBaMM 提供灵活框架,用于电池行为仿真、参数估计和实验设计,能快速构建并求解复杂的电化学与热物理模型。
- SALib (Sensitivity Analysis Library in Python):一个 Python 敏感性分析库,提供 Sobol、Morris、FAST 等方法。SALib 帮助理解模型输出对输入参数变化的敏感度,识别关键参数及交互作用,可用于模型参数不确定性量化和重要性排序。
代码实现
本项目基于 PyBaMM 的 SPMe(Single Particle Model with Electrolyte)模型,选取了正极厚度、负极厚度、隔膜厚度等典型几何参数,采用 SALib 的 Sobol 方法进行全局灵敏性分析。具体实现见 battery_model_sensitivity_analysis/notebooks/spme_geometric_sobol_analysis.ipynb。
量化时间序列差异
SPMe 模型输出(如电压)是时间序列数据。敏感性分析需量化参数变化后输出曲线 $Y(t)$ 与基准曲线 $Y_b(t)$ 间的差异,从如下角度考虑:
- 位置差异 ($\delta_p$): 衡量整体位置偏移。
$$\delta_p[Y(t), Y_b(t)] = \text{mean}[Y(t)] - \text{mean}[Y_b(t)]$$
- 尺度差异 ($\delta_s$): 衡量幅度差异。
$$\delta_s[Y(t), Y_b(t)] = (\max[Y(t)] - \min[Y(t)]) - (\max[Y_b(t)] - \min[Y_b(t)])$$
- 形状差异 ($\delta_r$): 衡量校正位置和尺度后的形状差异。在本研究中,我们使用均方根误差 (RMSE) 来量化形状差异:
$$\delta_r[Y(t), Y_b(t)] = \text{RMSE}(Y(t), Y_b(t)) = \sqrt{\frac{1}{M} \sum_{i=1}^{M} (Y(t_i) - Y_b(t_i))^2}$$
其中 $M$ 是评估时间点的数量。
本项目将采用综合差异指标 $\Delta_i = \delta_p + \delta_s + \delta_r$ 作为量化电压曲线 $V(t)$ 与基准电压曲线 $V_b(t)$ 之间综合差异的单一度量指标,并作为 Sobol 分析的目标函数输出。
import numpy as np
def calculate_combined_difference(Y, Y_b):
# 位置差异 (Position difference)
delta_p = np.mean(Y) - np.mean(Y_b)
# 尺度差异 (Scale difference)
delta_s = (np.max(Y) - np.min(Y)) - (np.max(Y_b) - np.min(Y_b))
# 形状差异 (Shape difference - RMSE)
delta_r = np.sqrt(np.mean((np.array(Y) - np.array(Y_b))**2)) # 确保Y, Y_b为numpy数组
# 综合差异 (Combined difference)
Delta_i = delta_p + delta_s + delta_r
return Delta_i
参数选取与范围设定
选定 SPMe 模型中的关键几何参数(如正极厚度、负极厚度、隔膜厚度),为每个参数设定合理的物理取值范围。
param_definitions = {
"Negative electrode thickness [m]": {
"default": default_param["Negative electrode thickness [m]"],
"bounds_factor": 0.2, # 变动 +/- 20%
},
"Positive electrode thickness [m]": {
"default": default_param["Positive electrode thickness [m]"],
"bounds_factor": 0.2,
},
"Separator thickness [m]": {
"default": default_param["Separator thickness [m]"],
"bounds_factor": 0.2,
},
"Negative particle radius [m]": {
"default": default_param["Negative particle radius [m]"],
"bounds_factor": 0.2,
},
"Positive particle radius [m]": {
"default": default_param["Positive particle radius [m]"],
"bounds_factor": 0.2,
},
}
problem = {
"num_vars": len(param_definitions),
"names": list(param_definitions.keys()),
"bounds": [],
}
for name, props in param_definitions.items():
lower_bound = props["default"] * (1 - props["bounds_factor"])
upper_bound = props["default"] * (1 + props["bounds_factor"])
problem["bounds"].append([lower_bound, upper_bound])
print(
f"Parameter: {name}, Default: {props['default']:.2e}, Bounds: [{lower_bound:.2e}, {upper_bound:.2e}]"
)
采样与仿真求解
利用 SALib 的采样工具(如 Saltelli 采样),在参数空间内生成大量参数组合。每组参数下,调用 PyBaMM 运行 SPMe 仿真,记录输出指标(如 1C 恒流充放电过程的终止电压、容量等)。
from SALib.sample import saltelli
# import pybamm # 假设pybamm已安装
# import numpy as np # 假设numpy已安装
# 生成参数样本
# N 通常取2的幂次,例如1024。样本总数将是 N * (D + 2) 或 N * (2D + 2)
# D 是参数数量 (problem['num_vars'])
param_values = saltelli.sample(problem, 1024)
# 运行一次基线仿真
model_baseline = pybamm.lithium_ion.SPMe()
param_baseline = pybamm.ParameterValues("Chen2020")
experiment_baseline = pybamm.Experiment(["Discharge at 1C until 2.5 V"])
sim_baseline = pybamm.Simulation(
model_baseline, experiment=experiment_baseline, parameter_values=param_baseline
)
sol_baseline = sim_baseline.solve()
t_eval_baseline = sol_baseline["Time [s]"].entries
voltage_baseline = sol_baseline["Terminal voltage [V]"].entries
# 为了确保所有仿真都在相同的时间点上进行比较,定义一个固定的时间向量 t_eval_common
# 使用基线仿真的最大时间,并插值到 200 个点
max_time_baseline = t_eval_baseline[-1]
t_eval_common = np.linspace(0, max_time_baseline, 200) # 200 个评估点
# 对基线解在 t_eval_common 上进行插值
voltage_baseline_interp = np.interp(t_eval_common, t_eval_baseline, voltage_baseline)
print(
"Baseline simulation complete and common evaluation time points (t_eval_common) prepared."
)
print(f"Baseline simulation ran for {max_time_baseline:.2f} seconds.")
print(
f"Common evaluation time points range from {t_eval_common[0]:.2f}s to {t_eval_common[-1]:.2f}s with {len(t_eval_common)} points."
)
def evaluate_model_delta_i(parameter_sample):
"""
运行 PyBaMM SPMe 模型并计算与基线电压曲线的综合差异指标 Delta_i.
Delta_i = delta_p + delta_s + delta_r
其中:
delta_p: 位置差异 (mean_run - mean_baseline)
delta_s: 尺度差异 ((max_run - min_run) - (max_baseline - min_baseline))
delta_r: 形状差异 (RMSE(run, baseline))
参数:
parameter_sample (np.array): SALib 生成的参数样本。
返回:
float: 电压曲线的综合差异指标 Delta_i。
"""
model_run = pybamm.lithium_ion.SPMe()
param_run = pybamm.ParameterValues("Chen2020") # 每次都从新的默认参数开始
current_params = {}
for i, name in enumerate(problem["names"]):
current_params[name] = parameter_sample[i]
try:
param_run.update(current_params)
sim_run = pybamm.Simulation(
model_run, experiment=experiment_baseline, parameter_values=param_run
)
sol_run = sim_run.solve(t_eval=t_eval_common)
voltage_run = sol_run["Terminal voltage [V]"].entries
if len(voltage_run) < len(t_eval_common):
padding_value = (
voltage_run[-1]
if len(voltage_run) > 0
else param_run["Lower voltage cut-off [V]"]
)
voltage_run_padded = np.full_like(t_eval_common, padding_value)
voltage_run_padded[: len(voltage_run)] = voltage_run
voltage_run = voltage_run_padded
# 计算 delta_p (位置差异)
delta_p = np.mean(voltage_run) - np.mean(voltage_baseline_interp)
# 计算 delta_s (尺度差异)
range_run = np.max(voltage_run) - np.min(voltage_run)
range_baseline = np.max(voltage_baseline_interp) - np.min(voltage_baseline_interp)
delta_s = range_run - range_baseline
# 计算 delta_r (形状差异 - RMSE)
delta_r = np.sqrt(np.mean((voltage_run - voltage_baseline_interp) ** 2))
# 计算综合差异指标 Delta_i
# 注意:直接相加可能会因为各项尺度不同导致某一项主导。可以考虑加权或归一化,但按当前要求直接相加。
delta_i = delta_p + delta_s + delta_r
# print(f"Run with {current_params}, d_p={delta_p:.3f}, d_s={delta_s:.3f}, d_r={delta_r:.3f}, Delta_i={delta_i:.3f}")
return delta_i
except Exception as e:
# print(f"Error during simulation with params {current_params}: {e}")
return 1e6 # 一个较大的惩罚值
灵敏性分析
将仿真结果输入 SALib 的 Sobol 分析模块,计算各参数的主效应指数(First-order Sobol index)、总效应指数(Total Sobol index)等灵敏度指标。
from SALib.analyze import sobol
# 执行 Sobol 分析
# Y_outputs 应为上一步仿真得到的实际输出结果数组
# 注意处理Y_outputs中的NaN值(如果仿真中可能出现)
# Y_outputs_cleaned = Y_outputs[~np.isnan(Y_outputs)]
# param_values_cleaned = param_values[~np.isnan(Y_outputs)]
# 如果清理了Y_outputs,对应的param_values也需要清理,但这会破坏Saltelli样本结构
# 更好的做法是在仿真失败时赋一个合理的惩罚值,而不是NaN,以保持样本完整性
Si = sobol.analyze(problem, Y_outputs, calc_second_order=True, print_to_console=False)
# 提取一阶和总效应指数
S1_indices = Si['S1']
ST_indices = Si['ST']
print("一阶 Sobol 指数 (S1):")
for name, s1_val in zip(problem['names'], S1_indices):
print(f"- {name}: {s1_val:.4f}")
print("\\n总 Sobol 指数 (ST):")
for name, st_val in zip(problem['names'], ST_indices):
print(f"- {name}: {st_val:.4f}")
# 如果 calc_second_order=True, 还可以获取二阶指数 Si['S2'] 和对应的参数对 Si['S2_conf']
结果可视化
最终计算结果下图所示:
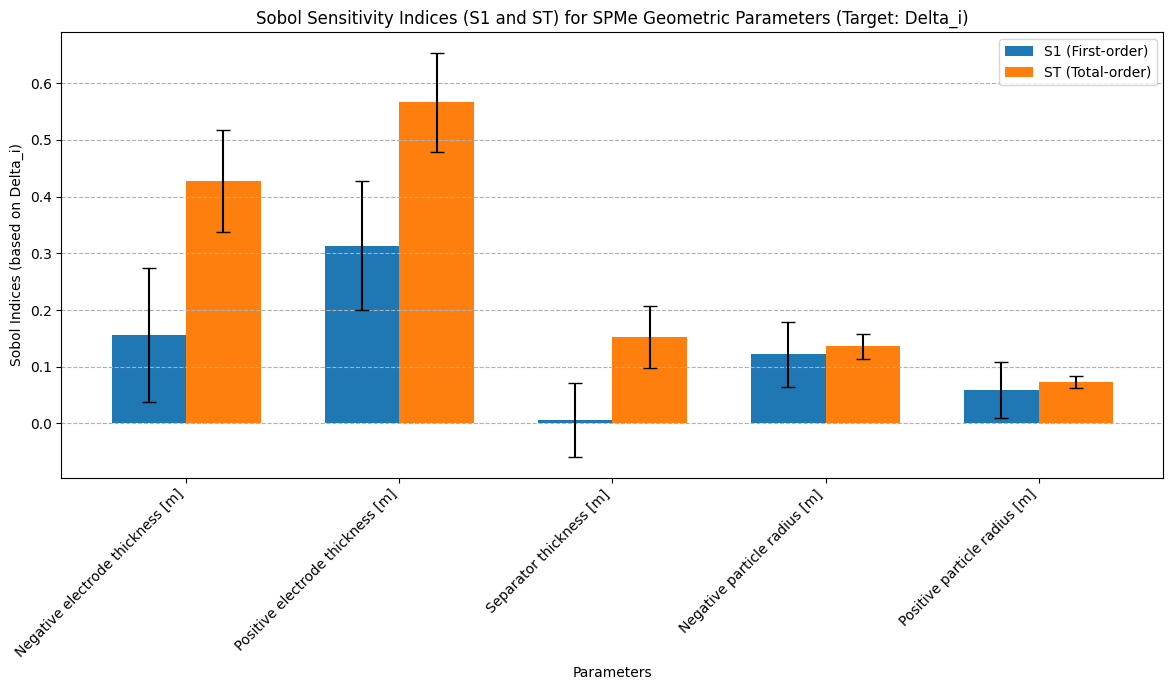
- 关键参数敏感性:部分参数(如
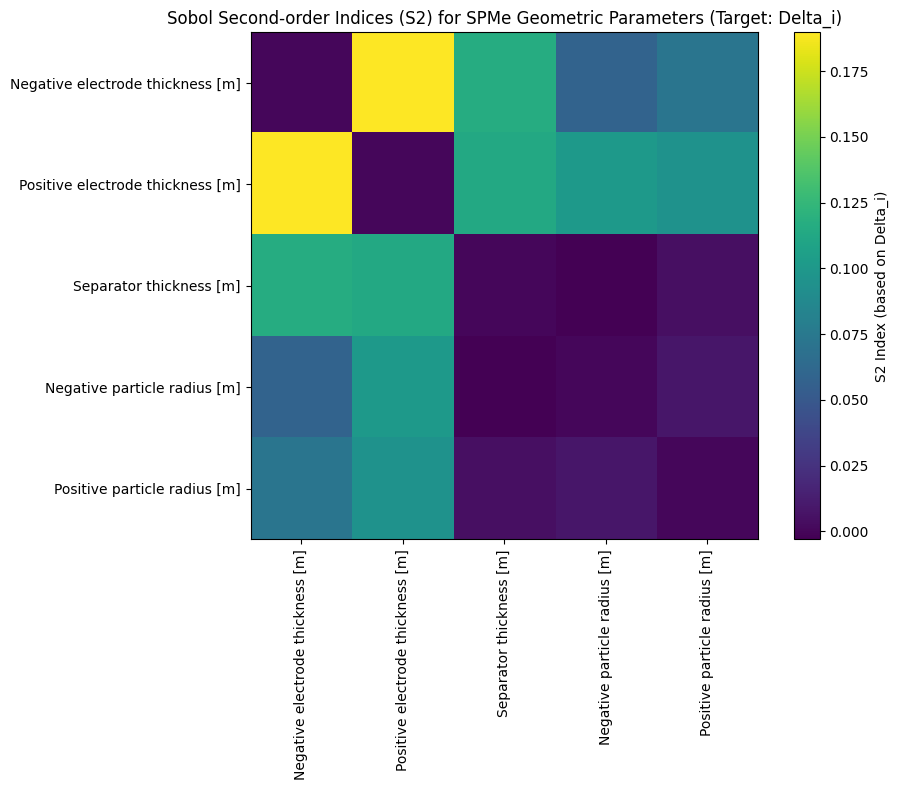
正极厚度、负极厚度)表现出最高的 S1 和 ST 值,它们对模型输出影响最为显著,是设计和制造中需精密控制的核心因素。 - 参数交互效应:S2 热力图显示特定参数对(如
正极厚度与负极厚度)之间存在较强 S2 值,这些参数间存在显著的交互作用。
相关文献同样指出,电池几何参数(尤其是电极厚度)对容量、功率密度等关键性能有重要影响。
- A Control-Oriented Simplified Single Particle Model with Grouped Parameter and Sensitivity Analysis for Lithium-Ion Batteries (2025) 通过 Sobol 灵敏性分析,将 SPM/ SPMe 的参数集从 9 个降至 6 个高敏感参数,电极厚度等几何参数位列其中。
- Global Sensitivity Methods for Design of Experiments in Lithium-ion Battery Context (2020) 也证实了几何参数在电池性能建模与实验设计中的重要性。
上述示例后续可以从增加分析的参数数量、精细化参数的采样范围、增加样本数量以及优化差异量化方法等进一步改进。